Regression Analysis Which Uses the Sum of the Squared Deviations
The table entitled ANOVA gives the sum of squares and the degrees of freedom in the column labeled df for the regression the residual and the total regression plus residual. The regression sum of squares SS_R is computed as the sum of squared deviation of predicted values hat Y_i with.

Standard Deviation Of Residuals Or Root Mean Square Deviation Rmsd Video Khan Academy
It shows how many points fall on the regression line.

. In this case we have sample data X_i and Y_i where X is the independent variable and Y is the dependent variable. Provided the regression function is appropriate the i-th squared residual from the OLS fit is an estimate of sigma_i2 and the i-th absolute residual is an estimate of sigma_i which tends to be a more useful estimator in the presence of outliers. From the practical point of view it means that with GNU R you can still use the lm function like in lmy x2 and it will work as expected.
Adds penalty equivalent to square of the magnitude of coefficients. In a regression analysis the goal is to determine how well a data series can be fitted to a function that might help to explain how the data series was generated. I am confused on the r-squared and Cohens d formula which uses the t value and square root of n.
The sum of squares is used as a. The mean square is given for the regression and the residual and the F-value and the associated p-value in the column labeled Sig is displayed. The fact the y is not linear versus x does not matter.
These results indicate that the regression is statistically. A key goal of regression analysis is to isolate the relationship between each independent variable and the dependent variable. So the procedure basically removes each observation and uses the model to predict that observation and squares the.
PRESS is similar except it is the sum of the squared deviations between the fitted value of each removed observation and the removed observation. So in the context of a linear regression analysis what is the meaning of a Regression Sum of Squares. Linear regression models are often fitted using the least squares approach but they may also be fitted in other ways such as by minimizing the lack of fit in some other norm as with least absolute deviations regression or by minimizing a penalized version of the least squares cost function as in ridge regression L 2-norm penalty and lasso L 1-norm penalty.
In computing the r-squared and Cohens d it appears as the sample size increases the effect size is less. Sum squared resid 1469535 Schwarz criterion 1935957 Log likelihood -3681397 F-statistic 8049775 Durbin-Watson stat 1971175 ProbF-statistic 0000000. For the above sample with 9df the r-squared.
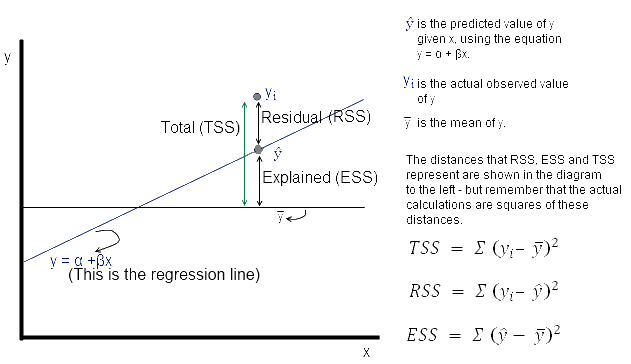
It can be shown to be equal to the square of the correlation between y_i and widehaty_i. The R 2 value is calculated from the total sum of squares more precisely it is the sum of the squared deviations of the original data from the mean. Our R-squared value equals our model sum of squares divided by the total sum of squares.
A good model has a model sum of squares and a low residual sum of squares. The model sum of squares is the sum of the squared deviations from the mean of Depend1 that our model does explain. The most common form of regression analysis is linear regression in which one.
Performs L1 regularization ie. The interpretation of a regression coefficient is that it represents the mean change in the dependent variable for each 1 unit change in an independent variable when you hold all of the other independent variables constant. The polynomial regression you are describing it is still a linear regression because the dependent variable y depend linearly on the regression coefficients.
It means that 91 of our values fit the regression analysis model. Working a problem with one study using 10 subjects having a t10 and comparing to another study with 100 subject also with a t19. CALIFORNIA STATE UNIVERSITY SACRAMENTO Guide ECON 200A.
Adds penalty equivalent to absolute value of the magnitude of coefficients. Minimization objective LS Obj α sum of square of coefficients Lasso Regression. It is the percentage of the total sum of squares explained by the model - or as we said.
Its the sum of the squared deviations between the the fitted values and the observations. The residuals are much too variable to be used directly in estimating the weights w_i so instead we use either the. Sum_i1n x_i - overlinex 0.
Well it is quite similar. Advanced Macroeconomic Theory Presentation of Regression Results Prof. The sum of the deviations from the mean is always equal to 0.
Beginalign R2dfracSSESST1-dfracSSRSST endalign which is called the R-squared of the regression. In our example R 2 is 091 rounded to 2 digits which is fairy good. Van Gaasbeck An example of what the regression table should.
In statistical modeling regression analysis is a set of statistical processes for estimating the relationships between a dependent variable often called the outcome or response variable and one or more independent variables often called predictors covariates explanatory variables or features. Therefore 0leq R2 leq 1. Performs L2 regularization ie.
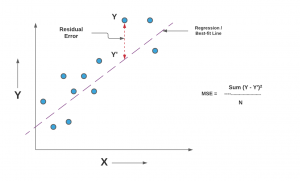
Mean Squared Error Or R Squared Which One To Use Data Analytics
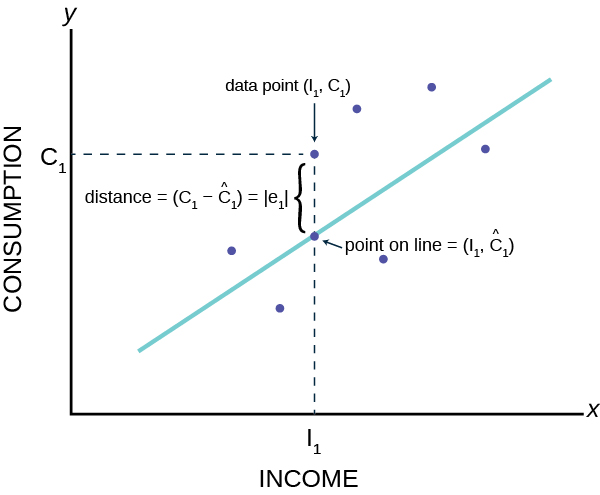
The Regression Equation Introductory Business Statistics
Regression Basics By Michael Brannick
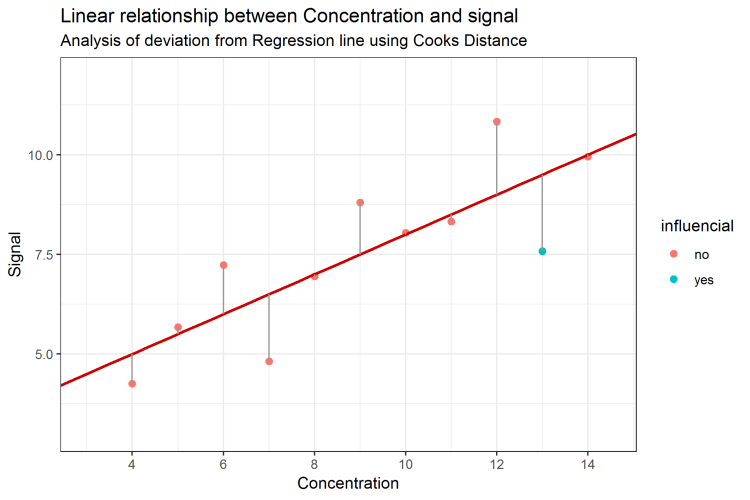
About Small Values With Huge Influence Sum Of Squares Part 2
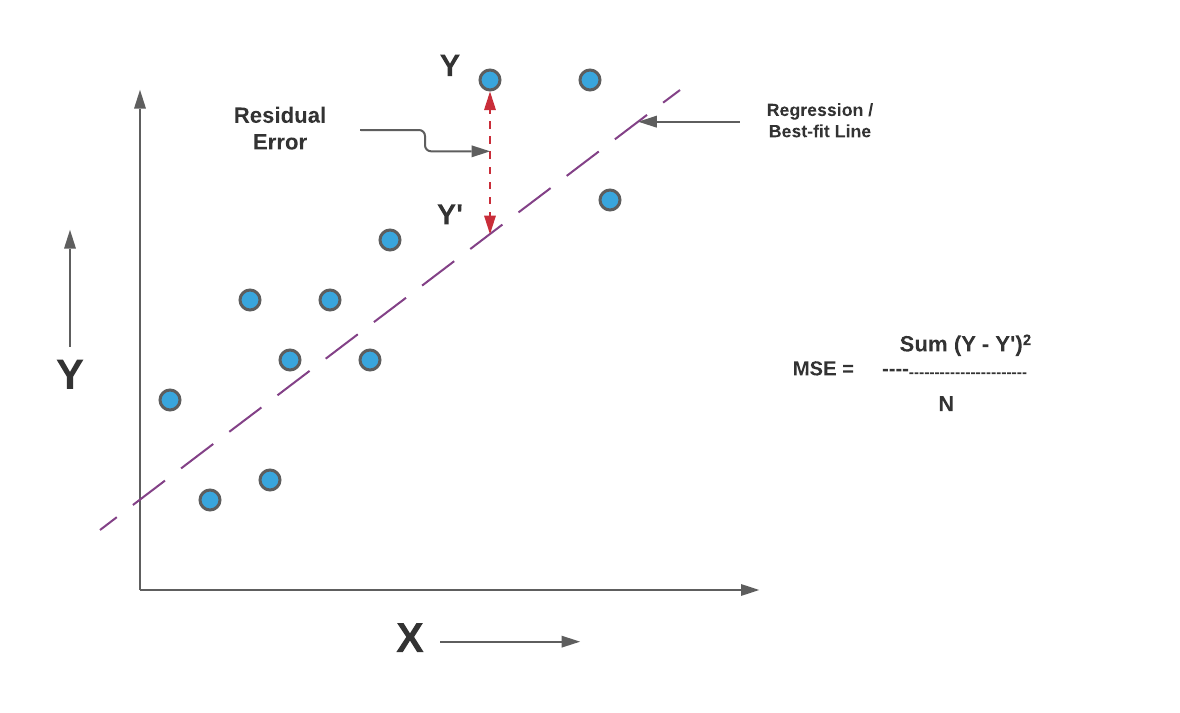
Mean Squared Error Or R Squared Which One To Use Data Analytics
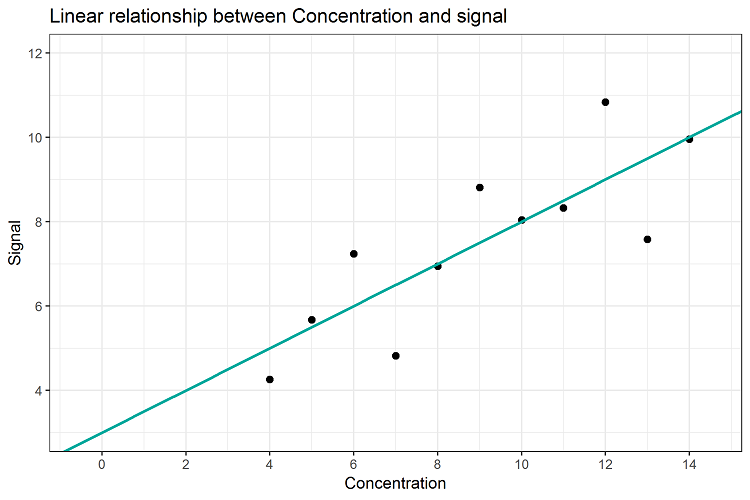
About Small Values With Huge Influence Sum Of Squares Part 1
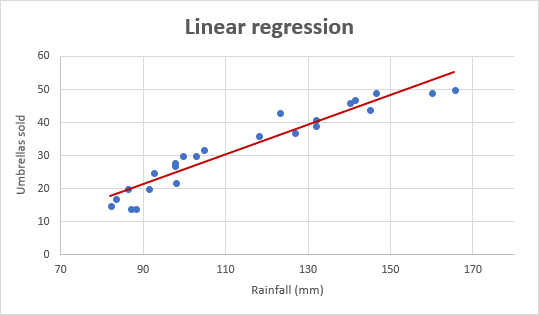
Linear Regression Analysis In Excel

Linear Regression With Sum Of Squares Formulas And Spreadsheet Use Youtube
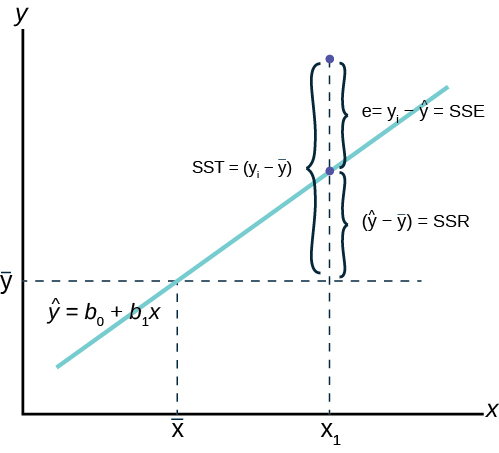
The Regression Equation Introductory Business Statistics

Alternative Sum Of Squares Formula Derivation Statistics Youtube
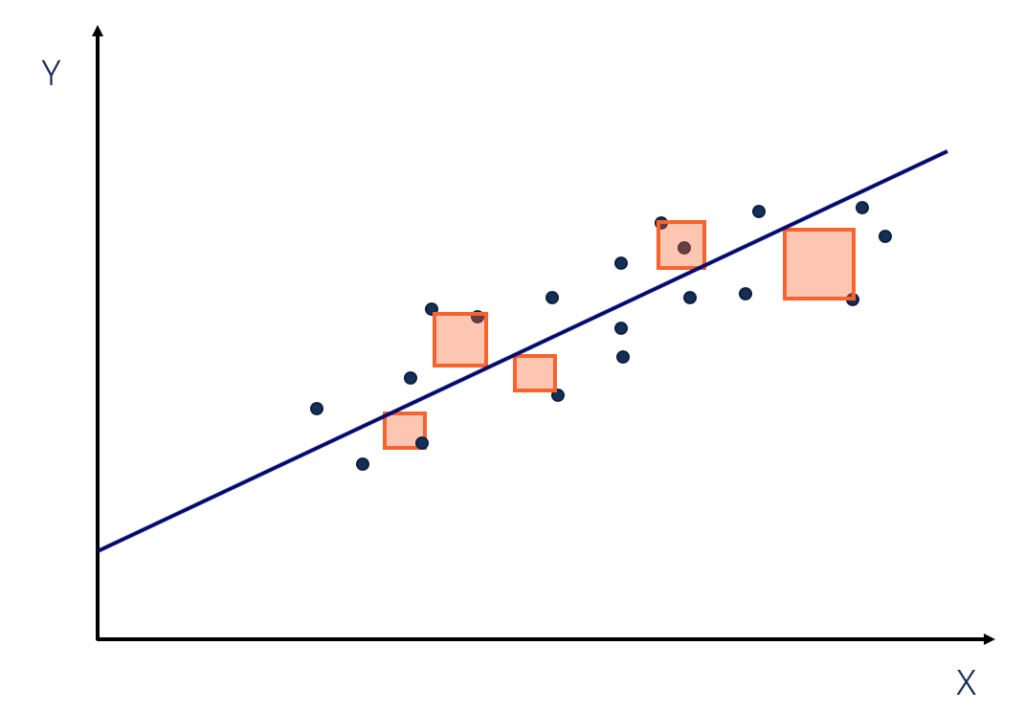
Sum Of Squares Definition Formulas Regression Analysis
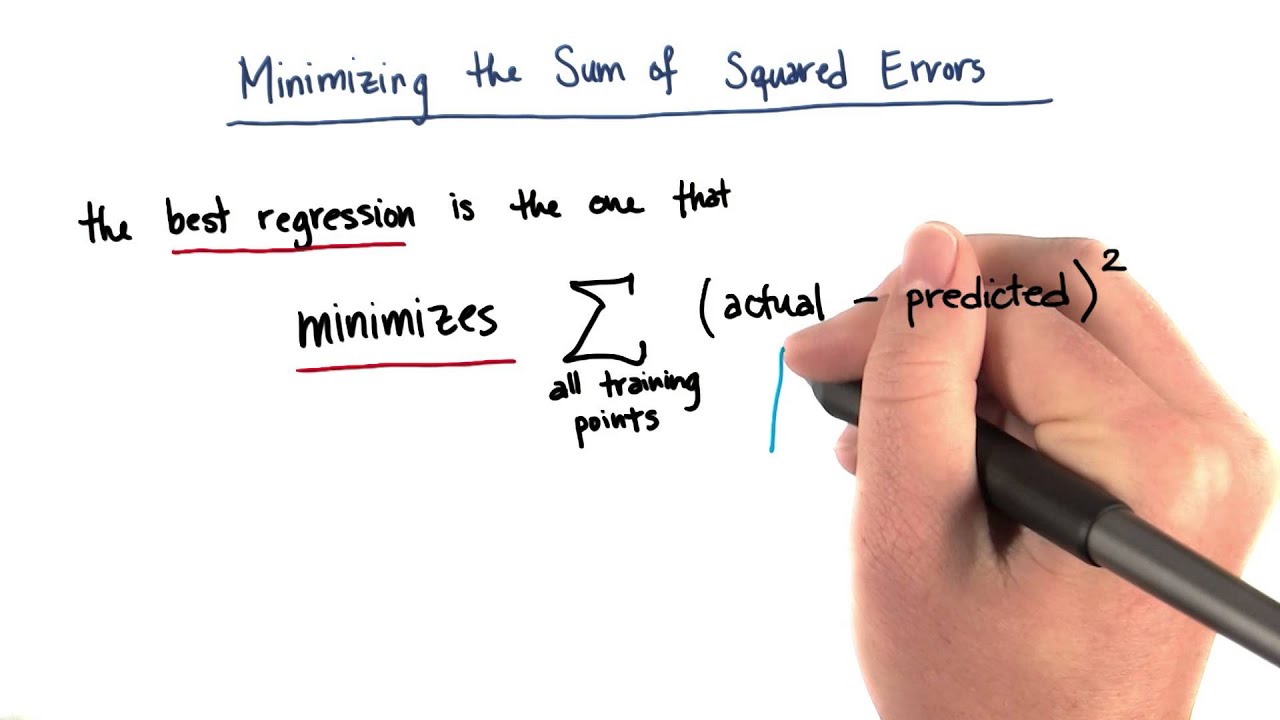
Minimizing Sum Of Squared Errors Youtube

How To Interpret Adjusted R Squared And Predicted R Squared In Regression Analysis Statistics By Jim

Residual Sum An Overview Sciencedirect Topics
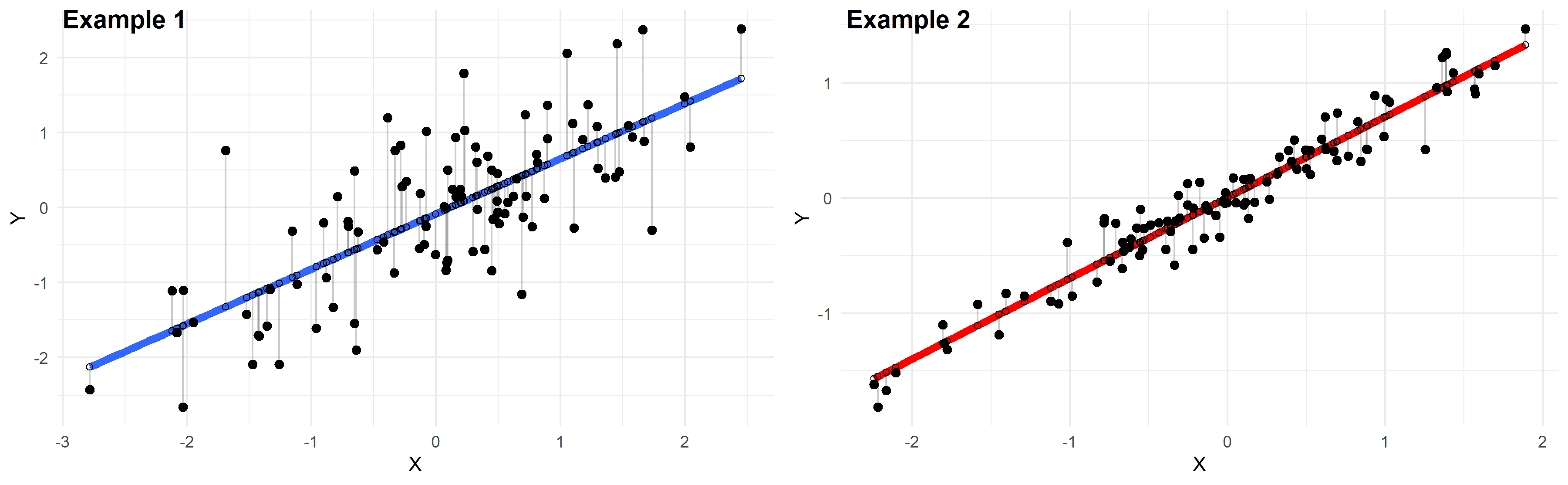
Residual Standard Deviation Error Guide For Beginners Quantifying Health
Step By Step Regression Analysis What Is Regression Analysis By Great Learning Medium

Comments
Post a Comment